1.3 Flow Regimes Based on Mach Number

The Mach number determines the qualitative behavior of a flow field and its interaction with surrounding geometry. Compressible flow regimes are classified as follows:

Subsonic Flow ( $M < 1$ )

Pressure disturbances can propagate upstream.
For $M < 0.3$ , compressibility is negligible.
Governing equations are elliptic in nature.
Typically smooth and predictable flow.

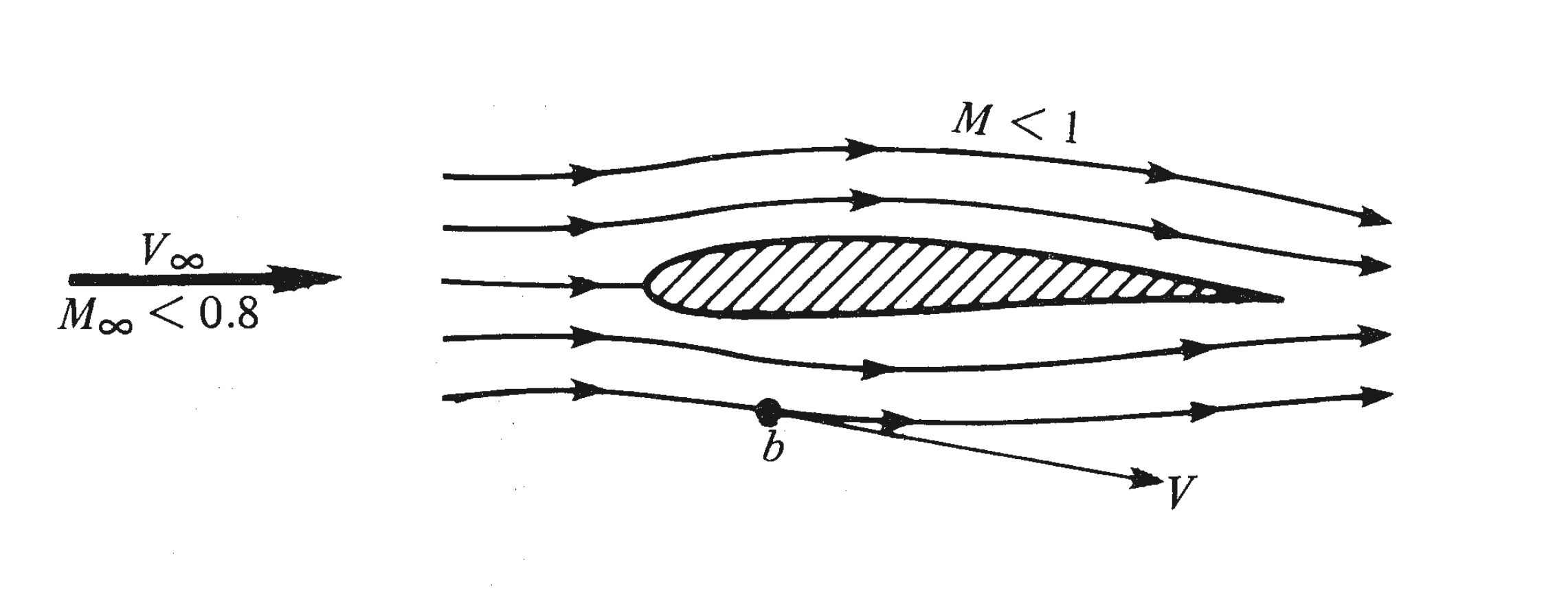
Subsonic flow is where M < 1 at every point, and hence, the flow velocity is everywhere less than the speed of sound. J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003. — Figure 1:Subsonic flow is where M < 1 at every point, and hence, the flow velocity is everywhere less than the speed of sound. Anderson (1990)
J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003.

Transonic Flow ( $0.8 < M < 1.2$ )

Contains both subsonic and supersonic zones.
Local shock waves and flow separation are common.
Highly sensitive to geometry and operating conditions.
Mixed-type governing equations (elliptic + hyperbolic).

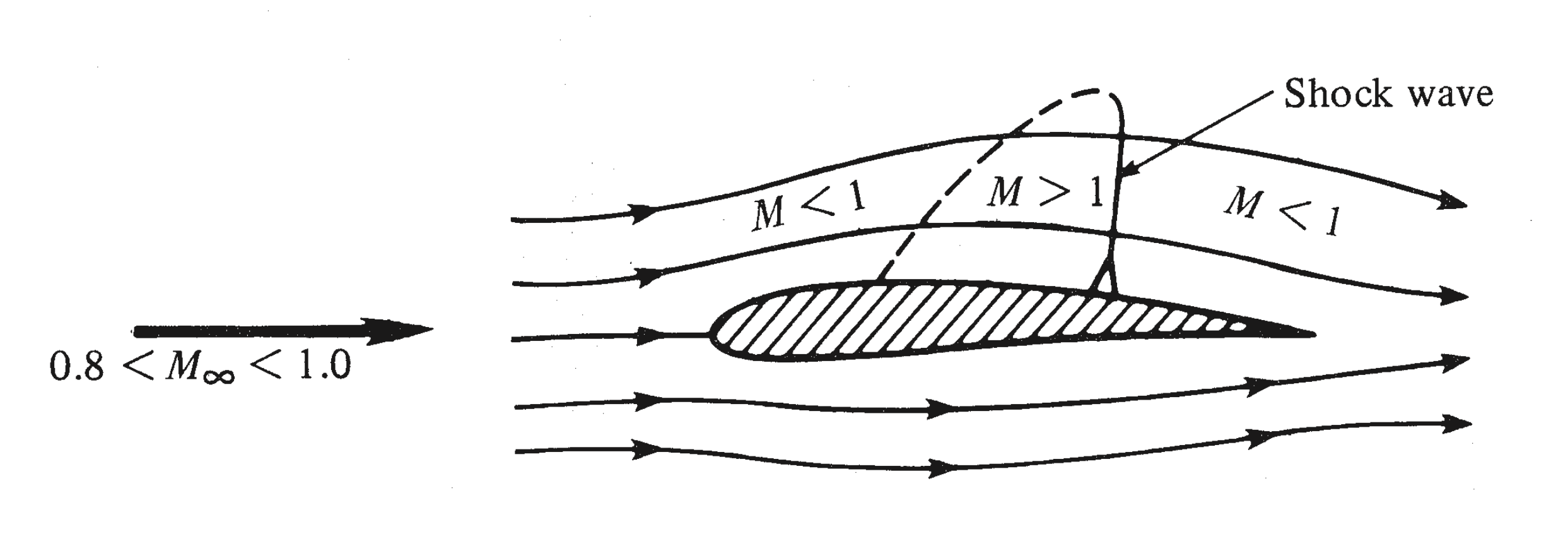
The local velocity and Mach number on the top surface increase above their free-stream values. For most of the airfoil it happen at mach number greater than 0.8 (not the rigid rule) and flow stream should remain subsonic. J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003. — Figure 2:The local velocity and Mach number on the top surface increase above their free-stream values. For most of the airfoil it happen at mach number greater than 0.8 (not the rigid rule) and flow stream should remain subsonic. Anderson (1990)
J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003.

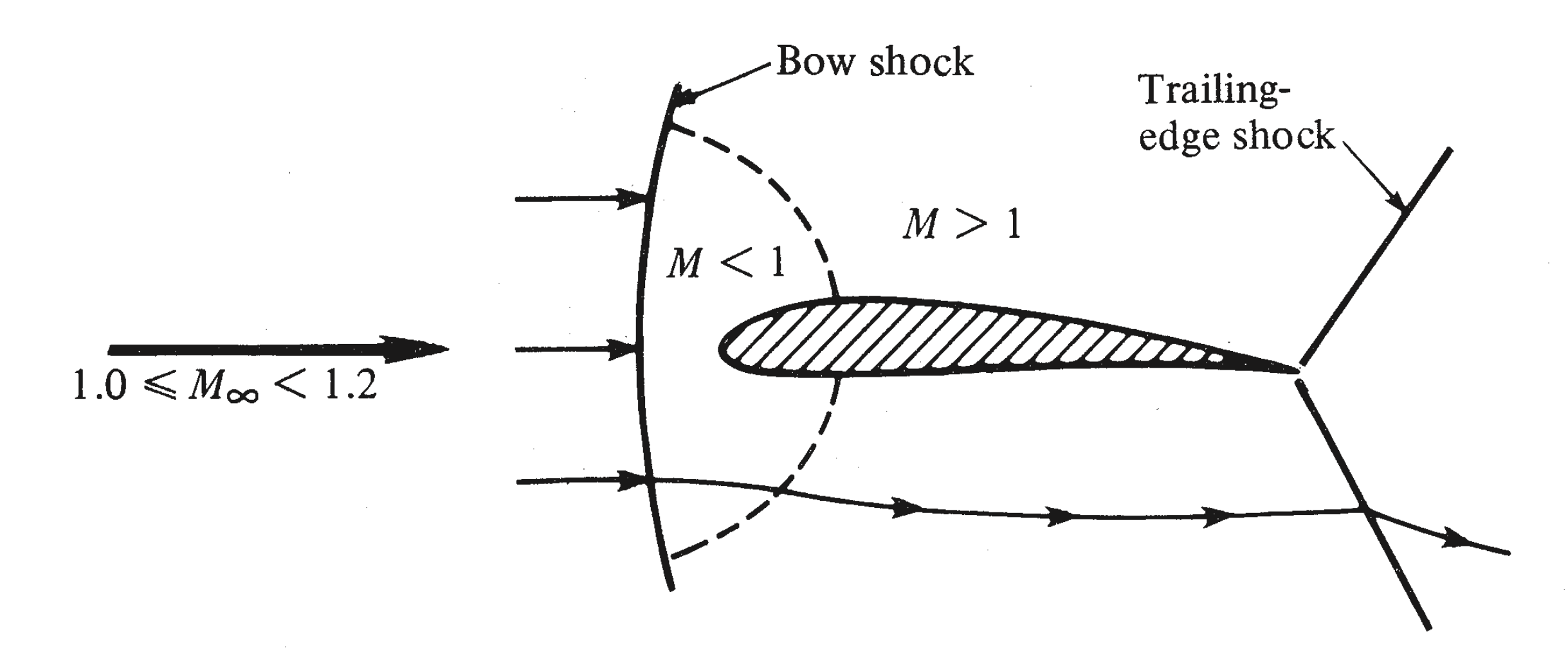
M_\infty is increased to slightly above unity, due to which the shock pattern moves to the trailing edge of the airfoil, and a second shock wave appears upstream of the leading edge. This second shock wave is called the bow shock. J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003. — Figure 3: $M_\infty$ is increased to slightly above unity, due to which the shock pattern moves to the trailing edge of the airfoil, and a second shock wave appears upstream of the leading edge. This second shock wave is called the bow shock. Anderson (1990)
J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003.

Supersonic Flow ( $M > 1$ )

Disturbances cannot propagate upstream.
Shock waves and expansion fans dominate flow structure.
Governing equations are hyperbolic.
Strong compressibility effects present.

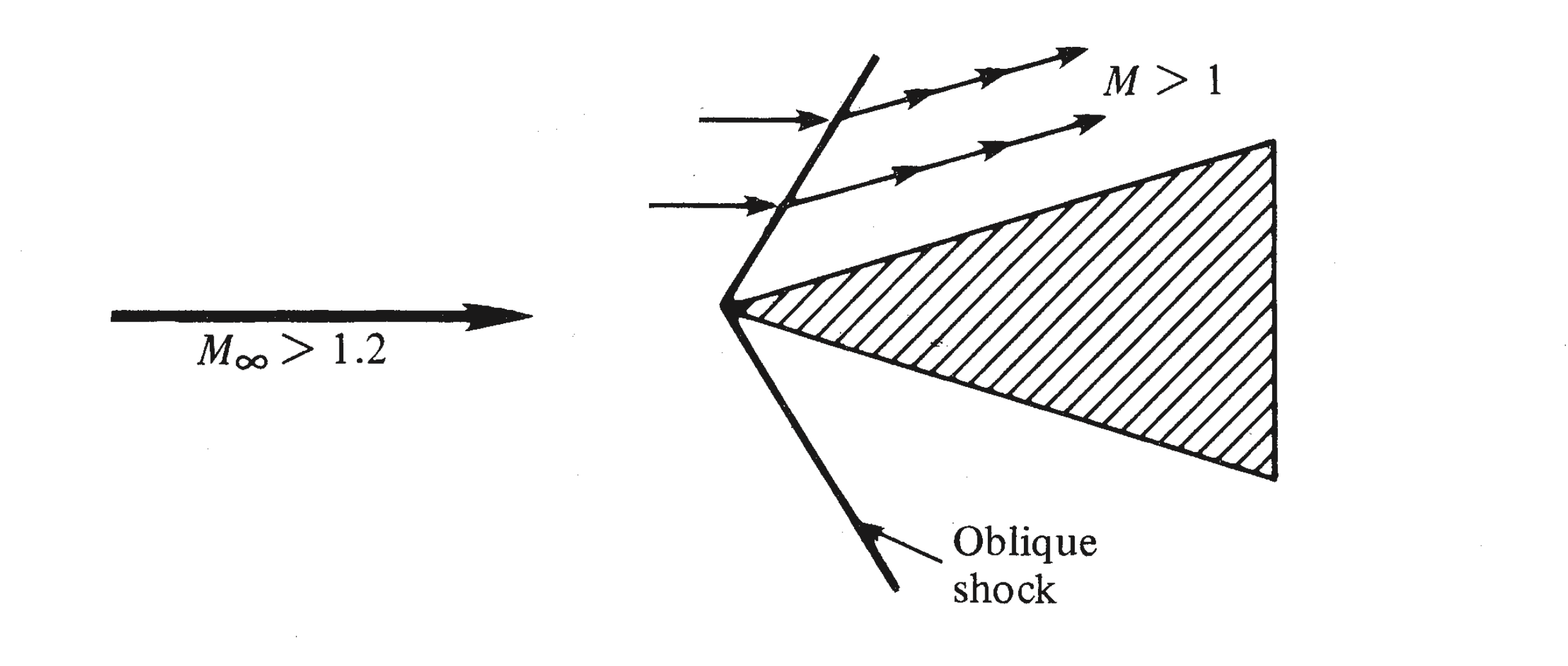
As the freestream mach number is increased, oblique shocks are formed. This shock wave is attached to the sharp nose of the wedge. Across this shock wave, the streamline direction changes discontinuously. Ahead of the shock, the streamlines are straight, parallel, and horizontal; behind the shock they remain straight and parallel but in the direction of the wedge surface. J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003. — Figure 4:As the freestream mach number is increased, oblique shocks are formed. This shock wave is attached to the sharp nose of the wedge. Across this shock wave, the streamline direction changes discontinuously. Ahead of the shock, the streamlines are straight, parallel, and horizontal; behind the shock they remain straight and parallel but in the direction of the wedge surface. Anderson (1990)
J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003.

Hypersonic Flow ( $M > 5$ )

Exhibits strong shock–boundary layer interactions.
Significant high-temperature effects:
- Vibrational excitation
- Molecular dissociation
- Chemical reactions
Requires thermochemical and viscous modeling.

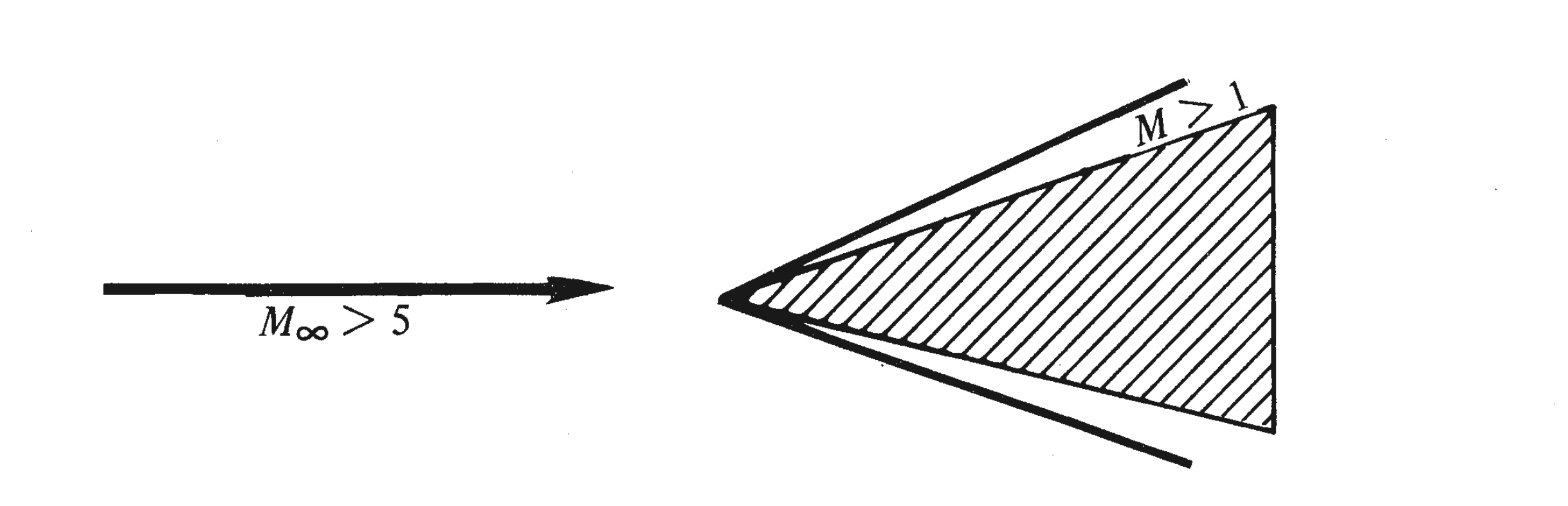
As M_\infty is increased to higher super- sonic speeds, the oblique shock wave moves closer to the surface J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003. — Figure 5:As $M_\infty$ is increased to higher super- sonic speeds, the oblique shock wave moves closer to the surface Anderson (1990)
J. D. Anderson, “Modern Compressible Flow with Historical Perspective,” Third Edition, McGraw Hill Professional, New York, 2003.

Flow Regime

Flow Regimes by Mach Number

Regime	Mach Number	Key Characteristics
Subsonic	$M < 1$	No shocks, upstream communication, low compressibility
Transonic	$0.8 < M < 1.2$	Local shocks, sensitivity, mixed-type PDEs
Supersonic	$M > 1$	Shock waves, expansion fans, hyperbolic behavior
Hypersonic	$M > 5$	Strong shocks, high-temperature effects, real-gas physics

References¶

Anderson, J. D. (1990). Modern compressible flow: with historical perspective. (None).

Supersonics

1.2 Mach Number and Compressibility

Supersonics

Chapter 2: Introduction to One-Dimensional Flows